Environmental Fluid Mechanics

Numerical Approximation of the 2D Shallow Water Equation (constant depth)

Above: 2D Shallow Water Equation (constant depth)
Above: Flow image with generated RGB color background, projected onto the surface generated from numerical approx. of the 2D Shallow Water Equation
Above: General form of the 2nd Order numerical approximation to the 2D Shallow Water Equation
Above: Shallow Water Equation with Impermeable Boundary Conditions (No Flux condition)

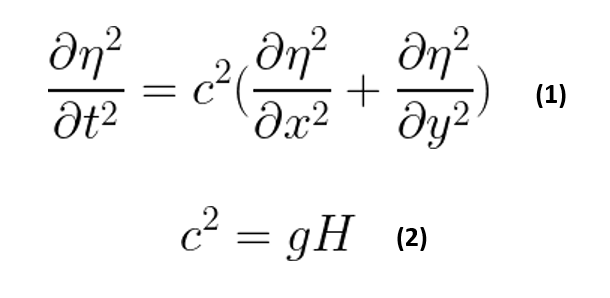
Details:
– 2nd Order (Explicit) approximation – central in time and space
– Forcing of Shallow Water Equation with damped oscillation at center of grid
– Implementation of Boundary Conditions (Neumann & Dirichlet Boundary Conditions) and Initial Conditions
– Coded through MATLAB

Numerical Approximation of the 2D exteneded Strecter-Phelps Equations

Above: Extended Strecter-Phelps Equations – 2D advection, diffusion, and reaction of Dissolved Oxygen and Biological Oxygen Demand
Above: list of variables in Strecter – Phelps Equations
Above: MATLAB surface plot (run to steady state) for the numerical approx. of the exteneded Strecter-Phelps equations
Above: Numerical approx. of DO and BOD levels, for a cross section running through the center-line of the stream

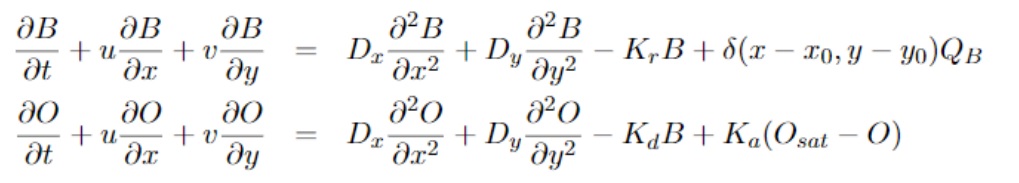
Details:
– Numerical approximation, first order in time and second order in space
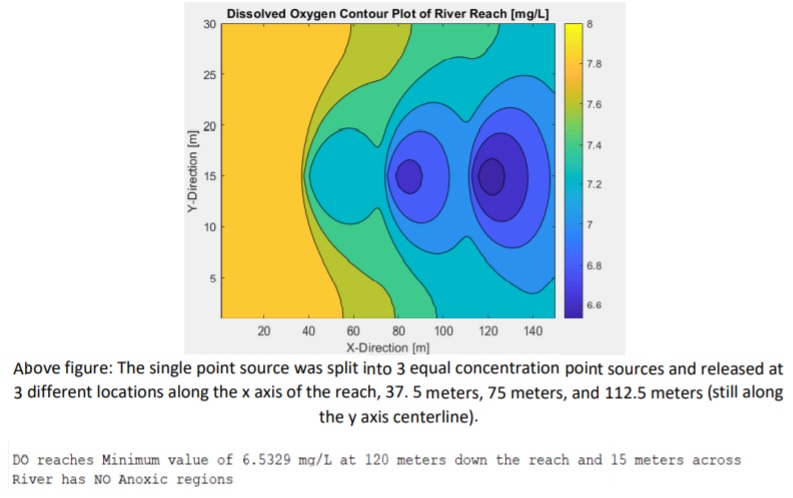
– Numerical solution of the PDE allows prediction of DO levels, when simulating the dumping of the pollutant (BOD)
-Von Neumann Stability Analysis: Peclet Number (Pe) must be 0 ā‰¤ Pe ā‰¤ 2
-Code displays ‘warning’ if anoxic conditions are reached (below 6 mg/L of DO)
-Allows engineers, scientist, and regulators the ability to optimize the disposal of waste (BOD), to avoid anoxic conditions (avoid violations/fines)


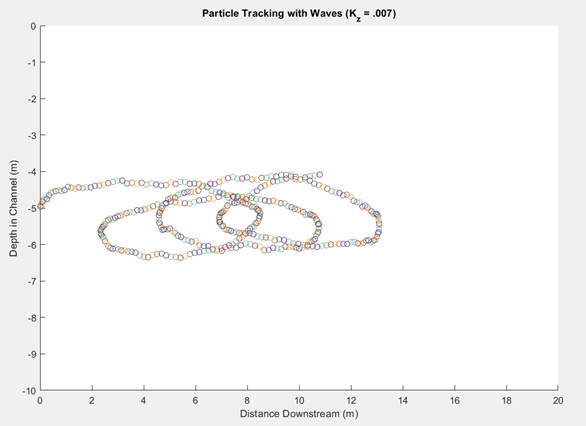
Stokes Drift with Turbulence


– Modeling of sediment transport, under the influence of waves & turbulence
– Three varying cases of turbulence investigated

Parameters
Wave period, T = 12 sec
Wave amplitude, a = 1 m
Water column depth, H = 10 m

Above: Three values of turbulent diffusivity investigated
Above: Idealized case (Stokes Drift without Turbulence) particles at higher levels in the water column drift further downstream; due to the larger magnitude of velocity in x & y direction

Above: Random nature of turbulence leads to a non-uniform dispersion of particles; particles forced upward due to turbulence will travel further downstream, while those forced downward will travel shorter distance

Details:
– Use of the Reynolds Average Navier- Stokes Equation (BGO/Mellor-Yamada 2-equation closure) to solve for velocity profile with incorporation of turbulence
-Increased turbulence leads to an increases in the variability of particle travel distance
-Model could be expanded to investigate other physical phenomena: influence of vegetation (increased roughness – shear stress), effect of salinity gradient (fresh and salt water interaction), and temperature gradient